[백준 1238] 파티

우선 이 문제는 굉장히 중요한 문제다.

최단거리 문제로 dijkstra 랑 floydwarshall을 이용해서 풀 수 있는데

둘 다 시간초과 나지 않고 풀 수 있다.

 

그리고 floydwarshall로 풀때는 일반적인 floydwarshall 써서 그대로 풀어주면 되는데

dijkstra는 살짝 새로운 접근방식으로 풀어야한다

 

일단 내 첫번째 풀이인 floydwarshall 부터 보고 

내가 게시판을 보고 깨달은 dijkstra 풀이법도 보자

 

---

[1. floydwarshall solution]

 

우선 두 가지를 파악할 수 있다

 

1. X 마을로 오고 가야함

2. 최단거리로 오고 가야함

 

이러면 최단거리 알고리즘인 다익스트라 벨만포드 플로이드 워셜 중 하나를 택하면 됨 ㅇㅇ

근데 시간이 무조건 양수이므로 일단 벨만포드를 쓸 명분은 없어짐

그리고 이게 모든 마을에 대한 모든 마을까지의 최단거리를 구하는게 훨씬 편함

그럼 a->x x->a 만 찾아서 더해주기만 하면 되기 때문

 

다익스트라 많이 돌려야할바에는 그냥 플로이드워셜로 한번에 구하는게 낫다는 것이다

다익스트라는 한 개의 특정 노드에 대해 다른 모든 노드까지의 최단거리를 구해주는 것이므로

이걸로 답 찾으려면 총 N번 돌려야함

그래서 그냥 플로이드워셜로 한번에 구하는게 낫다

 

사실 N<=1000 이여서

플로이드워셜로 3중포문 돌리면 1억이 넘어가 시간초과될 줄 알았으나 잘 통과됨 ㄷㄷ

 

INF 이면 그냥 계산하지 않고 스킵하는게 도움이 된듯 ㅇㅇ

아래의 if문을 넣어주면 시간이 반 정도 줄기 때문이다

// 거쳐가는 마을이 mid
	for (int mid = 1; mid <= N; mid++) {
		for (int s = 1; s <= N; s++) {
			if (dp[s][mid] == INF) continue;

			for (int e = 1; e <= N; e++) {
				dp[s][e] = min(dp[s][e], dp[s][mid] + dp[mid][e]);
			}
		}
	}

 

#include <iostream>
#include <algorithm>

#define SIZE 1001
#define INF int(1e9)

using namespace std;

int N, M, X;
int dp[SIZE][SIZE];

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);

	cin >> N >> M >> X;

	// init for floyd warshall
	for (int i = 1; i <= N; i++) {
		for (int k = 1; k <= N; k++) {
			dp[i][k] = INF;
		}
	}
	for (int i = 1; i <= N; i++) dp[i][i] = 0;

	int s, e, cost;
	for (int i = 0; i < M; i++) {
		cin >> s >> e >> cost;
		dp[s][e] = cost;
	}

	// 거쳐가는 마을이 mid
	for (int mid = 1; mid <= N; mid++) {
		for (int s = 1; s <= N; s++) {
			if (dp[s][mid] == INF) continue;

			for (int e = 1; e <= N; e++) {
				dp[s][e] = min(dp[s][e], dp[s][mid] + dp[mid][e]);
			}
		}
	}

	int ans = -1;
	for (int i = 1; i <= N; i++) {
		ans = max(ans, dp[i][X] + dp[X][i]);
	}

	cout << ans;
	return 0;
}

 

---

[2. dijkstra solution]

 

자 이제 두 번째 풀이인

dijkstra로 푸는 방법을 보자

 

아래는 내가 게시판을 보고

floydwarshall이 아닌 

모두가 다익스트라로 풀려는 것을 보고 올린 질문이고

그에 대한 답변이다

 

다익스트라를 거꾸로 해서 all to one이라 

이건 무슨 말이냐면

다음과 같이 그래프를 역전시킴으로써 모든 노드가 특정 노드로 가는 최단거리를 구할 수 있다는 애기

 

잘 생각해보면 말이 되는 얘기다

1에서 X로 가는 길이 있어서 1을 더하는거랑

X에서 1로 가는 길이 있어서 1을 더하는거랑

최종적으로 보면 같기 때문이다

 

 

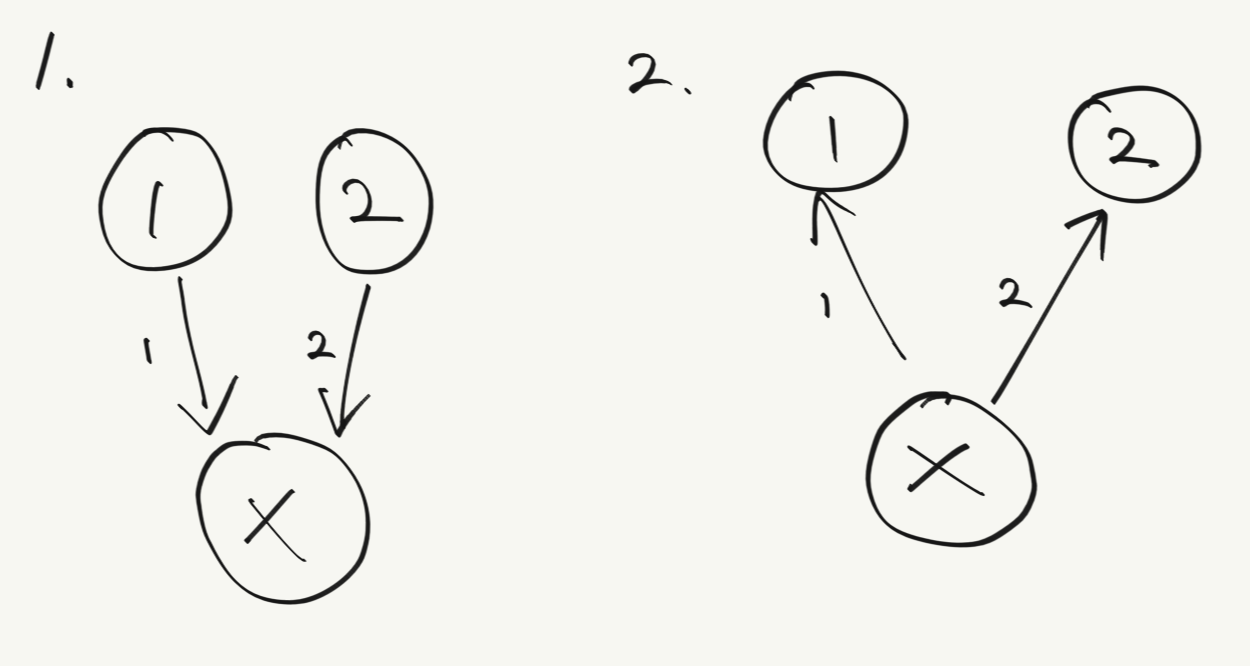
다익스트라는 단일 시작점을 기준으로 모든 정점 간의 최단 거리를 계산하기 때문에

1번같은 경우에 1,2 정점에서 X까지의 최단 거리를 구하려면 1,2 정점 각각에서 최단 거리를 구해야한다

하지만 이 경우는 매우 비효율적임

 

왜냐 각 노드에서 X까지의 최단거리만 구하고 싶은데

각 노드에서 모든 노드까지의 최단거리를 구하는 다익스트라를 N번 돌리는 것이기 때문이다

 

근데 이걸 2번처럼 간선을 역전시켜 역전 그래프를 만들면

1번의 상황, 즉 X까지의 최단거리를 구하기 위해

모든 노드에 대해 dijkstra를 돌려야하는 상황을

한번의 다익스트라 알고리즘을 통해서 해결할 수 있다

 

여기서 다음 코드가 정상그래프에 이은 역전그래프를 만드는 코드임

	int s, e, t;
	for (int i = 0; i < M; i++) {
		cin >> s >> e >> t;
		// X -> N(i) 위한 그래프
		real_graph[s].push_back(make_pair(e, t));
		// N(i) -> X 를 구하기 위한 역방향 그래프
		reversed_graph[e].push_back(make_pair(s, t));
	}

 

#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>

#define SIZE 1001
#define INF int(1e9)

using namespace std;

int N, M, X;

vector<vector<pair<int, int>>> real_graph(SIZE), reversed_graph(SIZE);

int* toX;
int* fromX;

int* dijkstra(int start, vector<vector<pair<int,int>>> graph) {
	int* ans = new int[N+1];

	// init to INF
	for (int i = 1; i <= N; i++) ans[i] = INF;
	
	// before dijkstra
	priority_queue<pair<int, int>, vector<pair<int,int>>, greater<pair<int,int>>> pq;
	pq.push(make_pair(0, start));
	ans[start] = 0;

	while (!pq.empty()) {
		int curnode = pq.top().second;
		int curcost = pq.top().first;
		pq.pop();

		for (int i = 0; i < graph[curnode].size(); i++) {
			int nextnode = graph[curnode][i].first;
			int cost = graph[curnode][i].second;

			// 우선순위큐에 넣어볼 가치가 있으면
            		// 즉 기존꺼보다 최단거리이면 최신화하고 우선순위큐에 넣어주기
			if (curcost + cost < ans[nextnode]) {
				ans[nextnode] = curcost + cost;
				pq.push(make_pair(curcost + cost, nextnode));
			}
		}
	}

	return ans;
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);

	cin >> N >> M >> X;
	
	int s, e, t;
	for (int i = 0; i < M; i++) {
		cin >> s >> e >> t;
		// X -> N(i) 위한 그래프
		real_graph[s].push_back(make_pair(e, t));
		// N(i) -> X 를 구하기 위한 역방향 그래프
		reversed_graph[e].push_back(make_pair(s, t));
	}

	toX = dijkstra(X, reversed_graph);
	fromX = dijkstra(X, real_graph);

	int ans = -1;
	for (int i = 1; i <= N; i++) {
		ans = max(ans, toX[i] + fromX[i]);
	}
	cout << ans;

	return 0;
}